(WIP) A more Realistic Scoring Mechinism for the I-Cut-You-Freeze Protocol.

An overview of gerrymandering and various attempts to fix it, plus my proposed idea to add more realism to a protocol attempting to make redistricting fair.

Introduction.

In the United States of America, local representatives are elected to the House of Representatives via direct local elections held in single-member districts. Each district is roughly equal in population, and the winner is decided via plurality. The Congressional districts of a state are redrawn every ten years following the United States census. The rules for redistricting vary from state to state, but all draw new Congressional maps via either their own state legislature, redistricting commissions, or through some combination of the two former.

As one might imagine, there is a great deal of partisan interest in the drawing of these maps. A rather extreme (yet very politically relevant) example of this is that of the redrawing of Florida’s congressional districts in 2022. In the state of Florida, the state legislature is to be responsible for redistricting proposals, which are then passed similarly to any other bill, to be approved by the governor prior to implementation. In the case of Florida, however, Republican Governor Ron DeSantis expressed general disapproval for proposals passed by the legislature, vetoing various proposals until the legislature expressed agreement regarding the consideration of a DeSantis-created proposal (one that shows a markedly favorable outcome in seats for the Republican Party). Such an event sets a dangerous precedent that may encourage other states to follow in Florida’s footsteps. In May 2022, the congressional map drawn by DeSantis’ staff has been deemed unconstitutional by a Florida state court judge, but the decision was later overturned by an appeals court. The state Supreme Court declined to weigh in on the decision stating that it was not their jurisdiction to rule on such matters. As a result, the DeSantis-created map will be in place for the 2022 elections. This tends to be the case with many redistricting proposals, if deemed unconstitutional it is often too late as they have already been used in at least one election.

Even in the case of “independent” redistricting commissions, there often exists some degree of partisan bias (even if this is justified through supposedly-equal representation in the commission from all relevant parties).

Due to the inherent partisan biases within the maps drawn for the legislature, there is no guarantee that the political makeup of the legislature will reflect the political composition of statewide vote casts in the election. For example, in the 2020 United States House of Representatives elections in Illinois, 57.10% of the population voted for the Democratic Party, yet Democratic representatives won 13 of the 18 district elections (72% of the seats). The Congressional map used in the election was drawn by the Illinois Democrats. Even worse, under the new map, Democrats are projected to win 14 of Illinois’ 17 congressional seats after the 2022 election (82% of the seats). This phenomenon is known as gerrymandering.

Gerrymandering is the process of constructing districts in such a way as to give your political party an advantage in elections. There are two principal tactics in gerrymandering, “packing” and “cracking.” Packing is when you create a single district that concentrates many voters of a single party in order to reduce that party’s voting power in other districts. Cracking is when you spread out the voting power of a party across many districts in order to dilute their overall voting power in certain districts. The overall goal is to pack opposition voters into some districts, effectively guaranteeing them some small number of government seats, while cracking across other districts in order to raise the chances of one’s own party gaining a high number of seats.

What are the implications of gerrymandering?

At this point, you may be asking yourself, “how did we get here? Why are only two parties duking it out for a select number of seats?” The root cause of the problem is in how representatives are elected. As mentioned previously, members of the House of Representatives (and state legislatures) elect their officials via direct local elections held in single-member districts where winners are chosen via a plurality ruling (sometimes referred to as first-past-the-post). Gerrymandering and the two-party system are very much a by-product of this system. Within political science, Duverger’s law states, “single-ballot plurality-rule elections (such as first-past-the-post) structured within single-member districts tend to favor a two-party system” (Wikipedia). Essentially, the system in place within the United States allows for minority parties with enough support to be grossly overrepresented. Once in power the ruling party is able to leverage gerrymandering while redistricting, leading to an even more unfair system where third parties are even more neglected. Eventually this leads to more strategic voting amongst voters to avoid the spoiler effect and the erosion of third parties. Two very good resources to see why this is the case are these two videos by CGP Grey: “Minority Rule: First Past the Post Voting”, and “Multiple Party Gerrymandering [Bonus Video]”.

Gerrymandering in algorithmic economics.

Gerrymandering in the field of Algorithmic Economics is generally viewed through the lens of cake cutting. For those unfamiliar, cake cutting tries to solve the problem of fairly dividing a heterogeneous, divisible good between several agents with different preferences. Naturally, one can see the connection to political districting and how cake cutting methods could be used to solve the problem of gerrymandering.

Related Works.

Cake cutting aside, there are several metrics to detect gerrymandering in congressional district maps. compares and contrasts several metrics for detecting gerrymandering, such as the efficiency gap. The efficiency gap was first introduced by and , with the goal of the setting a quantifiable, legal standard for what constitutes gerrymandering. The metric works off the notion of wasted votes. A wasted vote is any vote cast for the losing party in a district, or the winning party above a majority. The efficiency gap is calculated as the difference between the two parties’ wasted votes divided by the total number of votes. Most of the other metrics created are extensions on the efficiency gap, but ultimately, the efforts of this metric (and potentially others to come) failed when the Supreme Court rejected the standard in its 2018 decision in Gill v. Whitford.

In contrast to using methods to simply determine the fairness of districting proposals that were chosen under existing legal standards, there have been various protocols introduced that attempt to solve gerrymandering by finding a balance between two opposing partisan interests. The goal is to create a protocol by which there is no need to evaluate the fairness of a proposal, as the proposal is inherently fair to some degree prescribed by the protocol itself.

​ introduce a protocol that, following the nomenclature used by , we shall refer to as the LRY protocol. The overarching idea is to have one party divide one portion of a state into districts according to their own preferences, while the other party divides the rest of the state into districts with their own goals in mind. The thought is that having each party control some amount of the state yields a higher degree of fairness and satisfaction than other existing methods.

Issues arise, however, upon closer analysis of the LRY protocol. Through the analysis of it is seen that the results achieved by this protocol can be arbitrarily far from the geometric target. introduce the geometric target as a measure of fairness and is commonly used as a relaxation to the proportionality metric.

​ proposed a protocol with proven fairer outcomes. First, some notation. The state is defined as an interval $[0,n]$ (where $n$ is the number of districts). An $n$-districting is a set of $n$ disjoint subsets of the interval, each of size 1. The idea of votes in favor of one party is referred to as loyalty. If party A has 58% of the vote in a particular district, they are said to have a loyalty in that district of 0.58. The measure of the subset of $[0,n]$ loyal to Player 1 is denoted as $s_{1}^{n}$, and the measure of the subset of $[0,n]$ loyal to Player 2 is denoted as $s_{2}^{n}$. The slate of a player is the outcome from a districting, representing the number of districts loyal to them.

This protocol is structured such that two players take turns creating a $n$-districting and choosing which one of those $n$ districts they want to keep, or “freeze.” That district is then frozen, the roles swap, and the process continues, using the unfrozen area as the state.

The game resultant from this protocol can be represented recursively as follows, where $k=n$, $s_{1} = s_{1}^{n}$, and $A=1$, returning the slate of Player 1:

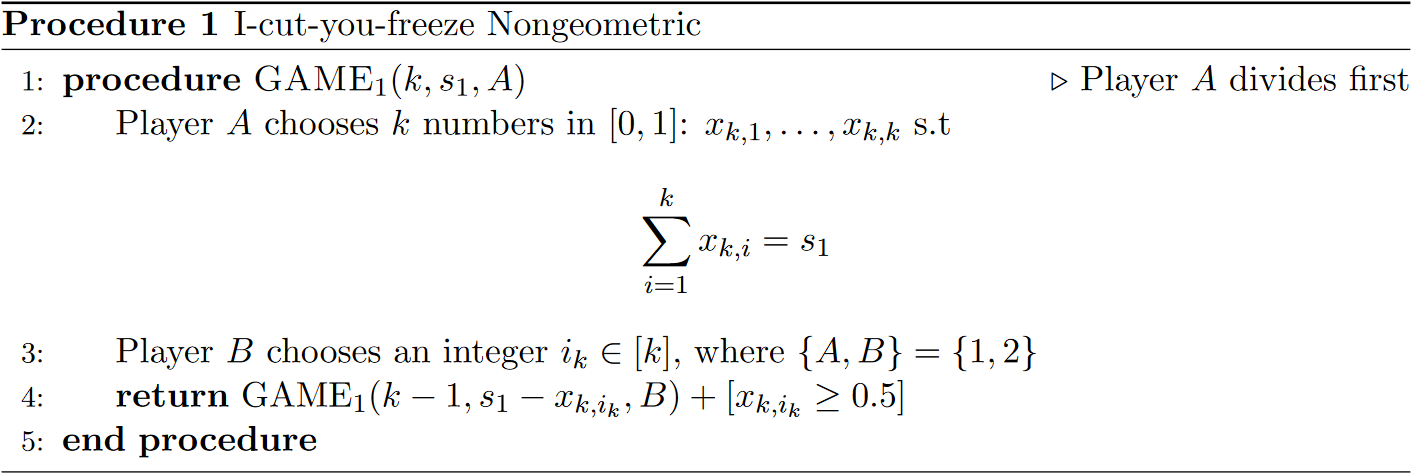
Let the unfrozen loyalties of Players 1 and 2 be $s_{1}^{(t)}$ and $s_{2}^{(t)}$, respectively, at the beginning of round $t$. The rounds begin at $n$ and count down to $0$, where the base case is defined as $\text{GAME}_{1}(0,0,A) = 0$. Note: the procedure always returns the slate of Player 1, even if $A = 2$.

A more realistic scoring mechinism.

One issue with the protocol above is that it assumes mapmakers are confortable with a narrow win. In reality this is not the case. To see this look at any of the state maps on FiveThirtyEight, you will see that a majority of districts are considered safe. Generally, districts drawn in the United States of America are drawn such that they are solidly Republican or Democrat, fewer districts slightly lean one way or the other, and an even smaller portion are competitive. Therefore, a general nondecreasing function $h:[0,1] \rightarrow [0,1]$ where $h(x)$ is the probability of winning a given district if you have x loyalty could be a more realistic choice for procedure 1. With a more general h function, the procedure output becomes the expected number of districts won by Player 1. A natural choice for this $h(x)$ function would be sigmoids of the form

\[h(x) = \frac{1}{1 + e^{-c(x - 0.5)}} ~ .\]

Where $c$ is a non-negative real number. Using the sigmoid function as our scoring mechanism, procedure 1 would become the following.

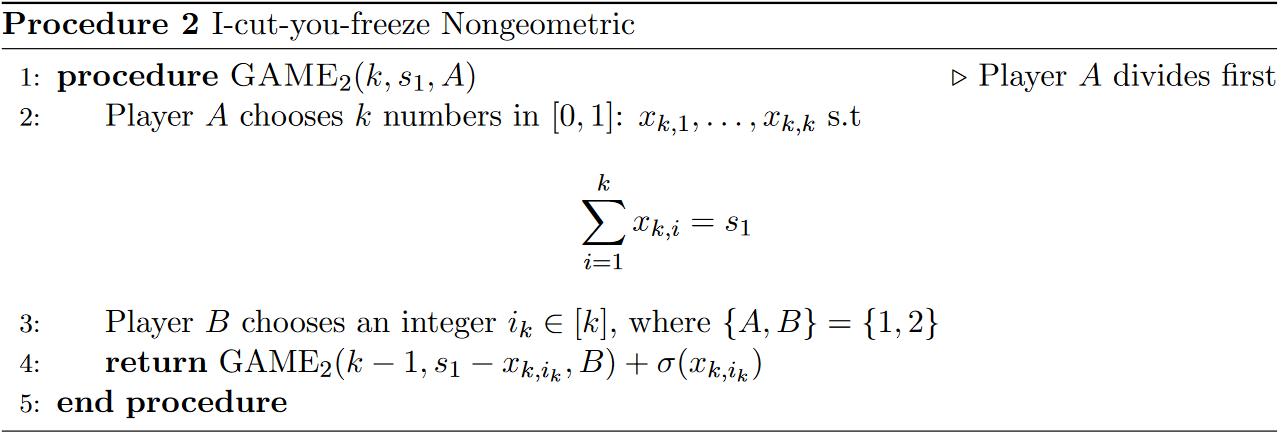
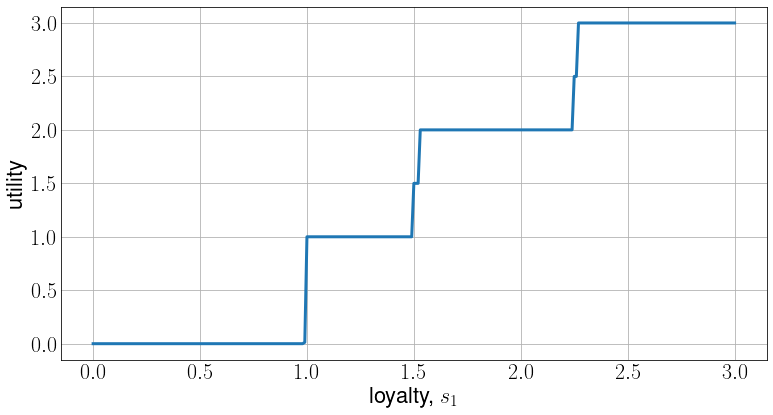
On property we would like to retain from the original procedure is that it is monotonically increasing with respect to $s_{1}$. It is important that any new I-cut-you-freeze procedure retain this property because with more loyalty your chances of winning more districts should only increase or stay the same. This is indead the case for any general nondecreasing function $h:[0,1] \rightarrow [0,1]$. The proof that any I-cut-you-freeze procedure using a general nondecreasing function $h:[0,1] \rightarrow [0,1]$ retains the monotonicity property is included in the appendix.

Empirical results.

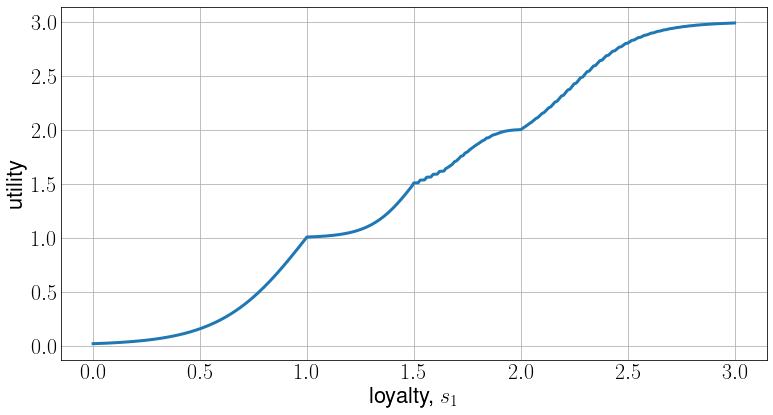
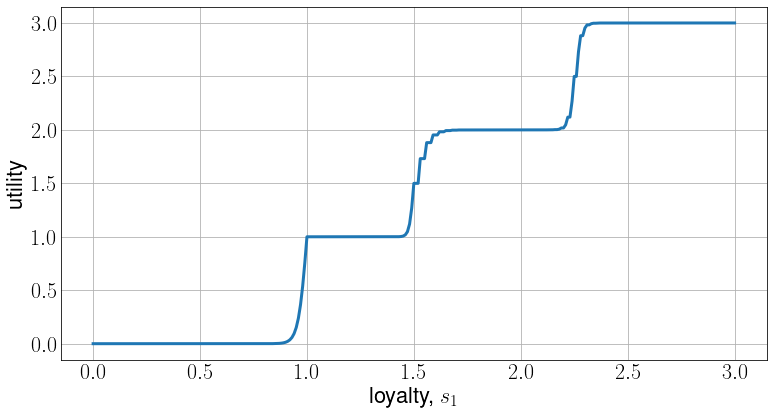
Appendix

The original paper written as a final project for Rafael Frongillo’s Algorithmic Economics class at the University of Colorado Boulder can be found here.

Proof that procedure 2 is monotonically increasing w.r.t. $s_{1}$.

Proof by Induction:

Let the function $f(k, s_1, A)$ be the output of $\text{GAME}_{2}(k, s_1, A)$ when the two players are playing optimally. Let $h(x)$ be a general nondecreasing function such that $h:[0,1] \rightarrow [0,1]$. Lastly, let \(\mathcal{X}_k(s) = \{ x_1 \dots x_k : x_i \in [0, 1], \sum x_i = s \}\). Then we have that

\[\begin{align} f(k, s_{1}, 1) &= \max_{x_{k,1},\dots,x_{k,k} \in \mathcal{X}_k(s_1)} \min_{i\in[k]}\left(f(k-1, s_{1}-x_{k, i}, 2) + h(x_{k, i})\right) ~ , \quad \text{and} \\ f(k, s_{1}, 2) &= \min_{x_{k,1},\dots,x_{k,k} \in \mathcal{X}_k(s_1)} \max_{i\in[k]}\left(f(k-1, s_{1}-x_{k, i}, 1) + h(x_{k, i})\right) ~ . \end{align}\]

Base Case:

Vascuous, $f(0, s_1, A) = f(0, 0, A) = 0$ by definition.

Inductive Hypothesis:

Fix $k$, $s_1$, and let $s_1 < s_1^\prime$. Let \(x_{k,1}^\star, \dots, x_{k,k}^\star\) be the optimal set of choices in (1). Let \(x_{k,1}^\dagger, \dots, x_{k,k}^\dagger \in \mathcal{X}_k(s_1^\prime)\) be the set of choices such that for all $i, ~ x_{k,i}^\star \leq x_{k,i}^\dagger$.

Note: for all $i$, \(s_{1} - x_{k,i}^\star \leq s_{1}^\prime - x_{k,i}^\dagger\), put another way, \(s_1^\prime - s_1 = \sum_i x_{k,i}^\dagger - x_{k,i}^\star\).

Inductive Step:

\[\begin{align*} f(k, s_{1}, 1) &= \min_{i\in[k]}\left(f(k-1, s_{1}-x_{k, i}^\star, 2) + h(x_{k, i}^\star)\right) \\ &\leq \min_{i\in[k]}\left(\underset{\text{By the inductive hypothesis}}{f(k-1, s_{1}^\prime-x_{k, i}^\dagger, 2)} + \underset{\text{By the monotonicity of } h(x)}{h(x_{k, i}^\dagger)}\right) \\ &\leq \max_{x_{k,1},\dots,x_{k,k} \in \mathcal{X}_k(s_1^\prime)} \min_{i\in[k]}\left(f(k-1, s_1^\prime-x_{k, i}, 2) + h(x_{k, i})\right) \\ &= f(k, s_{1}^\prime, 1) \end{align*}\]

Therefore, $f(k, s_{1}, A) \leq f(k, s_{1}^{\prime}, A)$ if $s_{1} < s_{1}^{\prime}$ via induction. Q.E.D.

Author Contributions.